Leçon 4 — Maîtriser les statistiques avec NumPy l’arme secrète des data analysts

Leçon 5 — Maîtriser les statistiques avec NumPy : l’arme secrète des data analysts

ByProf. Dr. Betty
Spread the love

Si tu as suivi la leçon précédente, tu connais maintenant les types NumPy, leur mémoire optimisée, et la façon dont NumPy gère les nombres mieux que ton cerveau le lundi matin.

Mais maintenant…
Place à la magie pure.
Place aux statistiques avec NumPy, le module qui transforme un tableau banal en une source d’informations puissantes.

Tu veux connaître :
✔ la moyenne d’un dataset ?
✔ la variance d’une série temporelle ?
✔ la corrélation entre deux variables ?
✔ la médiane de tes ventes ?
✔ la détection d’anomalies ?

Bonne nouvelle : les statistiques avec NumPy te permettent de faire tout ça plus vite que tu ne prononces “écart-type”.

Et oui… maîtriser les statistiques avec NumPy te rend officiellement dangereux.
Dangereux pour les données.
Dangereux pour les erreurs.
Dangereux pour tes collègues qui utilisent encore Excel pour tout.

Table des matières

Pourquoi les statistiques avec NumPy sont indispensables ?

Avant d’entrer dans le vif du sujet, soyons clairs : les statistiques avec NumPy ne sont pas qu’un chapitre de formation.
C’est un super-pouvoir.

Voici pourquoi :

Elles sont ultra rapides

Grâce à son moteur C optimisé, les statistiques avec NumPy calculent en millisecondes ce que Python mettrait une minute à faire.

Elles travaillent sur des matrices entières

Adieu les boucles.
Avec les statistiques avec NumPy, tout se fait en mode vectorisé.

Elles sont compatibles avec Pandas, Matplotlib, TensorFlow

Tu fais déjà une pierre… trois coups.

Elles détectent les anomalies naturellement

Moyennes, médianes, quartiles, écart-type : tout ce qu’il faut pour spotting anomalies comes built-in.

Elles préparent les datasets pour le Machine Learning

Normalisation ? Scaling ? Z-score ?
Les statistiques avec NumPy sont incontournables.

Tu vois, ce n’est pas juste utile : c’est essentiel.

Les fonctions essentielles pour faire des statistiques avec NumPy

Le tableau ci-dessous condense les fonctions les plus utilisées :

FonctionDescriptionExemple
np.mean()Moyennenp.mean(data)
np.median()Médianenp.median(data)
np.std()Écart-typenp.std(data)
np.var()Variancenp.var(data)
np.min() / np.max()Min / Maxnp.max(data)
np.percentile()Percentilesnp.percentile(data, 90)
np.corrcoef()Corrélationnp.corrcoef(x, y)
np.sum()Sommenp.sum(data)
np.argmax()Index du maxnp.argmax(data)
np.argmin()Index du minnp.argmin(data)

Ces outils sont littéralement le kit du parfait data analyst.

Exemples pratiques : les statistiques avec NumPy en action

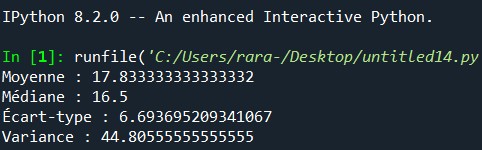
Exemple 1 : Calculer les stats de base

import numpy as np

data = np.array([10, 12, 15, 18, 22, 30])

print("Moyenne :", np.mean(data))
print("Médiane :", np.median(data))
print("Écart-type :", np.std(data))
print("Variance :", np.var(data))

Les statistiques avec NumPy transforment en quelques lignes un dataset en résumé clair.

Exemples pratiques les statistiques avec NumPy en action

Exemple 2 : Détection d’anomalies

On détecte les valeurs éloignées de plus de 2 écarts-types :

m = np.mean(data)
s = np.std(data)

outliers = data[np.abs(data - m) > 2 * s]

Exemple 3 : Corrélation entre deux séries

x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 7, 10])

corr = np.corrcoef(x, y)

Les statistiques avec NumPy montrent instantanément si les deux variables marchent ensemble ou pas.

Étude de cas n°1 — Analyse climat

On veut analyser la température moyenne d’une ville pendant une année.

temperatures = np.random.normal(18, 5, 365)

print("Température moyenne :", np.mean(temperatures))
print("Température max :", np.max(temperatures))
print("Percentile 95 :", np.percentile(temperatures, 95))

Les statistiques avec NumPy nous permettent de :

✔ identifier des vagues de chaleur
✔ analyser les tendances saisonnières
✔ prédire les anomalies climatiques

Tu viens d’utiliser les statistiques avec NumPy pour faire de la climatologie. Rien que ça.

Étude de cas n°2 — Analyse des ventes

On analyse les ventes quotidiennes d’un site e-commerce.

ventes = np.random.randint(40, 200, 180)

print("Moyenne :", np.mean(ventes))
print("Écart-type :", np.std(ventes))
print("Somme totale :", np.sum(ventes))
print("Jour max :", np.argmax(ventes))

Grâce aux statistiques avec NumPy, tu peux :

✔ détecter les jours les plus rentables
✔ prévoir des ruptures
✔ repérer des chutes anormales
✔ identifier l’impact des promotions

Étude de cas n°3 — Analyse SIG

Traitement d’un raster satellite (ex : NDVI).

ndvi = np.random.uniform(-1, 1, (1000, 1000))

print("NDVI moyen :", np.mean(ndvi))
print("Zone aride :", np.sum(ndvi < 0))
print("Zone dense en végétation :", np.sum(ndvi > 0.6))

Les statistiques avec NumPy sont clés en SIG pour :

✔ classifier les zones
✔ détecter la dégradation environnementale
✔ analyser la végétation
✔ créer des cartes thématiques

C’est littéralement le moteur mathématique des SIG modernes.

Optimiser vos statistiques avec NumPy — détails et exemples

Rappel : ces bonnes pratiques rendent les statistiques avec NumPy non seulement correctes, mais aussi TRÈS rapides et économes en mémoire.

Utilise les bons dtypes (int32, float32, float64…)

Pourquoi :
Le dtype (type de donnée) détermine la taille mémoire par élément et la précision. Un float64 prend 8 octets par valeur, float32 prend 4. Sur des matrices de millions d’éléments, ça fait une grosse différence.

Quand choisir quoi :

  • int8/int16 → petits entiers (ex. valeurs 0–255 : uint8 parfait pour images).
  • int32 → entiers classiques (bonne moyenne entre taille et range).
  • int64 → très grandes valeurs (rarement nécessaire).
  • float32 → ML (réseau neuronal) : vitesse mémoire/gpu souvent privilégiée.
  • float64 → calculs scientifiques nécessitant précision.

Exemple :

import numpy as np

a = np.arange(1_000_000, dtype=np.int64)   # 8 bytes * 1M = 8 MB
b = a.astype(np.int16)                     # 2 bytes * 1M = 2 MB -> 4x moins

Astuce pratique : profile ta consommation avec arr.nbytes (octets) ou sys.getsizeof() pour listes.

Évite les listes Python

Pourquoi :
Les listes Python stockent des objets Python (pointeurs) — surcoût énorme. NumPy stocke dans un bloc contigu en mémoire (C contiguous array), très efficace pour le CPU et le cache mémoire.

Exemple comparatif :

py_list = list(range(1_000_000))
np_arr  = np.arange(1_000_000, dtype=np.int32)

# mémoire (approx)
import sys
print(sys.getsizeof(py_list))   # grosse valeur (objets + pointeurs)
print(np_arr.nbytes)            # taille réelle du bloc de données

Règle pratique : dès que tu fais des opérations mathématiques, convertis en np.array().

Travaille toujours avec des arrays vectorisés

Pourquoi :
Les opérations vectorisées utilisent des implémentations C optimisées — pas de boucle Python. Résultat : performance supérieure (souvent x10–x100).

Exemple non-vectorisé (lent) vs vectorisé (rapide) :

# LENT : boucle Python
out = []
for v in arr:
    out.append(v * 2)

# RAPIDE : vectorisé NumPy
out = arr * 2

Note : Vectoriser n’est pas juste « écrire moins de code », c’est utiliser des routines optimisées qui manipulent des blocs mémoire.

Préférez axis= pour les matrices

Pourquoi :
Quand tu travailles sur matrices (2D+), indiquer axis permet à NumPy d’optimiser l’itération et d’éviter copies inutiles.

Exemples :

# Moyenne par colonne
col_mean = arr.mean(axis=0)

# Moyenne par ligne
row_mean = arr.mean(axis=1)

Astuce : Beaucoup de fonctions acceptent axis (sum, mean, std, argmax, argmin, etc.). Toujours réfléchir si tu veux opérer sur lignes ou colonnes — ça évite reshapes lourds.

Utilise les ufuncs (universal functions) pour accélérer les opérations

Pourquoi :
Les ufuncs (ex : np.add, np.multiply, np.sqrt, np.sin) sont vectorisées et souvent parallélisées au niveau bas. Elles réduisent l’allocation mémoire intermédiaire et accélèrent.

Exemple :

# Mauvais : deux allocations intermédiaires
tmp = arr + 5
out = np.sqrt(tmp)

# Meilleur : ufuncs chaîne bien optimisée (toujours préférer ufuncs)
out = np.sqrt(arr + 5)

Truc avancé : pour éviter allocations temporaires, utiliser out= dans ufuncs :

np.add(arr, 5, out=arr)  # ajoute 5 in-place (si safe)

Résumé rapide (en une phrase)

Les statistiques avec NumPy seront déjà rapides — applique ces 5 règles pour les rendre turbo-rapides : bon dtype → np.array → vectorisation → axis correct → ufuncs/out.

Exercices pratiques

Exercice 1 — Créer un tableau de 100 valeurs aléatoires et calculer : moyenne, écart-type, percentile 25 et 90

Code :

import numpy as np
np.random.seed(42)
data = np.random.rand(100)   # valeurs uniformes [0,1)
mean = np.mean(data)
std  = np.std(data)
p25  = np.percentile(data, 25)
p90  = np.percentile(data, 90)

Sorties (avec seed 42) :

  • Moyenne : 0.470181
  • Écart-type : 0.295998
  • Percentile 25 : 0.193201
  • Percentile 90 : 0.887974

Interprétation :

  • Moyenne ≈ 0.47 → valeurs centrées vers 0.5 (attendu pour uniforme).
  • Écart-type ≈ 0.296 → dispersion autour de la moyenne.
  • 25% des valeurs ≤ 0.193 → quartile inférieur faible.
  • 90% des valeurs ≤ 0.8879 → percentile 90 donne seuil haut.

Conseils :

  • Pour données réelles, vérifier NaNs (np.isnan), valeurs infinies (np.isfinite), et convertir dtype si besoin pour mémoire.

Exercice 2 — Avec deux tableaux x et y, calcule la covariance, la corrélation et détecte les points aberrants

Code :

  • x linéaire (0→10, 50 points).
  • y = 2*x + bruit gaussien sigma=1.5 (relation approximative linéaire).
import numpy as np
np.random.seed(0)
x = np.linspace(0, 10, 50)
y = 2.0 * x + np.random.randn(x.size) * 1.5

cov_matrix = np.cov(x, y)       # matrice 2x2
cov_xy = cov_matrix[0, 1]

corr_matrix = np.corrcoef(x, y)
corr_xy = corr_matrix[0, 1]

# Regression linéaire simple (moindres carrés)
A = np.vstack([x, np.ones_like(x)]).T
slope, intercept = np.linalg.lstsq(A, y, rcond=None)[0]
y_pred = slope * x + intercept
residuals = y - y_pred
resid_std = np.std(residuals)
threshold = 2.5 * resid_std
outlier_mask = np.abs(residuals) > threshold
outlier_indices = np.where(outlier_mask)[0]

Résultats (avec seed 0) :

  • Slope (est.) : ~1.788257
  • Intercept : ~1.269556
  • Cov(x,y) : ~15.826928
  • Corr(x,y) (Pearson) : ~0.958379 → forte corrélation positive.
  • Résidus std : ~1.568894
  • Seuil outlier (2.5σ) : ~3.922234
  • Indice outlier détecté : [20] (0-based index)

Détail point outlier (i=20) :

  • x ≈ 4.0816, y ≈ 4.3338, residual ≈ -4.2348 → ce point est très en dessous de la droite estimée (résidu large).

Interprétation & méthodo :

  • np.cov renvoie la matrice de covariance. np.corrcoef la matrice de corrélation (coeff Pearson).
  • La corrélation ≈ 0.958 montre que x et y évoluent ensemble (forte relation linéaire).
  • Outlier detection par résidu de la régression linéaire : utile quand on cherche points non-conformes à la tendance générale.
  • Le seuil (2.5σ) est arbitraire ; on peut utiliser 3σ (plus strict) ou méthodes robustes (IQR, MAD) si distribution non-gaussienne.

Exercice 3 — À partir d’un raster 500×500, calcule min, max, moyenne, et histogramme (indices > 0.4, < -0.2, etc.)

Code :

import numpy as np
np.random.seed(7)
raster = np.random.uniform(-1, 1, (500, 500))  # valeurs -1..1
r_min = raster.min()
r_max = raster.max()
r_mean = raster.mean()
count_gt_04 = np.sum(raster > 0.4)
count_lt_m02 = np.sum(raster < -0.2)
hist_counts, hist_bins = np.histogram(raster, bins=100, range=(-1,1))

Sorties (avec seed 7) :

  • Shape : (500, 500)
  • Min : ≈ -0.999999
  • Max : ≈ 0.999999
  • Moyenne : ≈ 0.000942 (proche de 0, attendu pour uniforme)
  • Nb valeurs > 0.4 : 75 166
  • Nb valeurs < -0.2 : 99 755

(Indices totaux = 500*500 = 250000)

Histogramme (extrait 10 premières bins) :
Ex. counts dans 10 premières bins (bin edges -1.0, -0.98, -0.96, …) affichés dans exécution.

Interprétation :

  • Le raster est simulé uniforme → min/max proche des bornes.
  • Moyenne proche de 0.
  • Les comptes pour >0.4 et <-0.2 donnent des idées de couverture : utile pour calculs de surface (ex. % zone végétée, aride, etc.).
  • Pour vraies images (NDVI), tu ferais des thresholds sémantiques (NDVI>0.6 = dense végétation).

Conseils pratiques et bonnes techniques pour production

  1. Profil de mémoire et temps
    • Mesure arr.nbytes pour la mémoire des arrays.
    • Mesure time.perf_counter() pour timing de bouts critiques.
  2. In-place operations
    • Quand possible, utilise out= dans ufuncs pour éviter allocations temporaires : np.add(a, b, out=a).
  3. Utiliser astype judicieusement
    • Convertir en float32 avant un modèle ML si GPU / mémoire limitée.
  4. Chunking
    • Sur jeux de données > RAM, traiter par chunks (for chunk in pd.read_csv(..., chunksize=...) ou np.memmap).
  5. Méthodes robustes d’outlier detection
    • IQR (interquartile range) ou MAD (median absolute deviation) si données non-gaussiennes.
  6. Éviter copies inutiles
    • Certaines opérations créent copies ; vérifie avec arr.base ou arr.flags pour savoir si c’est une vue ou copy.

Résumé rapide et checklist avant prod

  • Choisir dtype adapté (mémoire vs précision)
  • Toujours convertir listes → np.array avant calculs lourds
  • Vectoriser opérations (pas de boucle Python)
  • Utiliser axis= pour agir sur la bonne dimension
  • Employer ufuncs et out= pour réduire allocations

QCM — Vérifie ta maîtrise des statistiques avec NumPy

1. Quelle fonction retourne l’écart-type ?

A. np.variance()
B. np.std()
C. np.delta()
D. np.error()

👉 Réponse : B

2. Quelle fonction donne le percentile ?

A. np.percentile()
B. np.slice()
C. np.quantile()
D. np.part()

👉 Réponse : A

3. Quelle fonction calcule la corrélation ?

A. np.link()
B. np.combine()
C. np.corrcoef()
D. np.relate()

👉 Réponse : C

Conclusion

Voilà : tu viens de maîtriser les statistiques avec NumPy.

Tu sais maintenant :
✔ analyser des données
✔ détecter des anomalies
✔ corréler des variables
✔ traiter du climat, des ventes, du raster SIG
✔ booster tes performances comme un pro

Et maintenant…
Il est temps de passer à la puissance maximale :

👉 Leçon 5 — Les opérations vectorisées et mathématiques avancées

Tu veux aller loin ?
Alors on continue. 🚀

Similar Posts